Czym jest splątanie kwantowe i dlaczego nie posłuży nam do nadświetlnej komunikacji?

Wyobraź­cie sobie nastę­pu­ją­cą sytu­ację. Wasz kolega robi mały pokaz: rzuca na raz dwiema mone­ta­mi, a te za każdym razem lądują dając odwrot­ny wynik. Kiedy jedna upada do góry reszką, na drugiej zawsze widzi­cie orzełka. Jeżeli udałaby mu się ta sztuka wie­lo­krot­nie, powiedz­my dzie­sięć razy z rzędu, zdro­wo­roz­sąd­ko­wo uzna­li­by­śmy, że mamy do czy­nie­nia z czymś dziwnym. Jeżeli nato­miast kolega osią­gnął­by bliź­nia­czy wynik sto razy, musie­li­by­śmy oskar­żyć go o jakiś szwindel. 

Rachu­nek praw­do­po­do­bień­stwa pod­po­wia­da nam, że rezul­ta­ty rzutów powinny być losowe. Przy dzie­siąt­kach lub setkach prób, wyniki orzeł-reszka, reszka-reszka, orzeł-orzeł, powinny wypadać mniej więcej z równą czę­sto­tli­wo­ścią. Wyraźny odchył w którąś stronę oznacza, że z mone­ta­mi coś jest nie tak. Że wystę­pu­je tu zagad­ko­wa syn­chro­ni­za­cja, a jedna w jakiś sposób pozo­sta­je zwią­za­na z drugą.

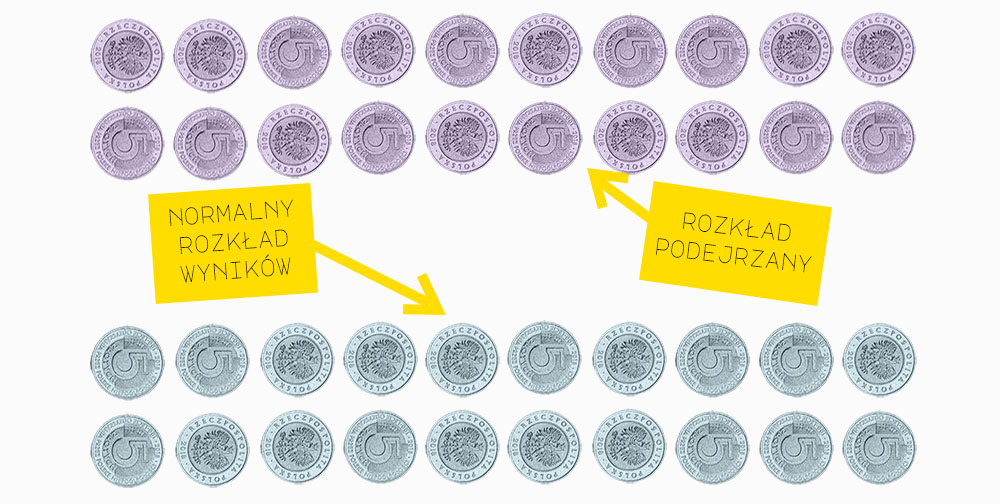
Splątanie kwantowe dla początkujących

Mniej więcej podobne zja­wi­sko badają od niemal stu­le­cia fizycy kwan­to­wi. Oczy­wi­ście splą­ta­nie kwan­to­we, jak zwykło się o nim mówić, nie dotyczy rzutów pię­cio­zło­tów­ka­mi, lecz pomia­rów nie­któ­rych wła­ści­wo­ści cząstek sub­a­to­mo­wych. W prak­ty­ce naj­le­piej radzimy sobie ze splą­ty­wa­niem fotonów, czyli cząstek światła. Metod jest wiele. Fizycy potra­fią np. pod­sma­żyć laserem atom odpo­wied­nie­go pier­wiast­ka, pobu­dza­jąc jego elek­tro­ny do emisji fotonów zorien­to­wa­nych pod prze­ciw­nym kątem. Mogą również prze­pu­ścić wiązkę lasera przez spe­cjal­ny krysz­tał prze­pusz­cza­ją­cy połowę fotonów, a połowę odbi­ja­ją­cy na bok.

Bez względu na tech­ni­kę, teoria kwan­to­wa zakłada, że chociaż mamy do czy­nie­nia z dwoma oddziel­ny­mi foto­na­mi, ich stan pozo­sta­nie ze sobą sko­re­lo­wa­ny. Ale to jeszcze nic! Splą­ta­na para fotonów będzie dzie­li­ła wspólny los, bez względu na dzie­lą­cą oba kwanty odle­głość. Ujmując to meta­fo­rycz­nie, nawet jeżeli jedną monetą rzucamy na Ziemi, a drugą na Marsie – nadal doświad­czy­my tajem­ni­cze­go powią­za­nia wyników.

Pierw­szy teo­re­tycz­ny opis tego efektu spo­rzą­dził Albert Ein­ste­in wraz z dwoma kole­ga­mi, Borisem Podol­skim i Natha­nem Rosenem już w 1935 roku. Trzej fizycy byli jednak mocno scep­tycz­ni i spe­ku­lo­wa­li na temat splą­ta­nia po to, aby wykazać, że takie zja­wi­sko nie powinno wystę­po­wać w przy­ro­dzie, a teoria kwan­to­wa musi być dziu­ra­wa. Dziś wiemy, że byli oni w ogrom­nym błędzie.

Cząstki to nie rękawiczki

Co tak napraw­dę draż­ni­ło twórcę teorii względ­no­ści? Wyobraź­my sobie, że mamy do dys­po­zy­cji dwie spla­ta­ne, ale zamknię­te w pudeł­kach cząstki, które wysy­ła­my na różne planety, albo nawet do oddziel­nych galak­tyk. Kiedy otwo­rzy­my jedno z nich i zoba­czy­my foton spo­la­ry­zo­wa­ny pionowo, od razu będzie­my wie­dzie­li, że foton zamknię­ty w drugim pojem­ni­ku powi­nien być zorien­to­wa­ny odwrot­nie, czyli poziomo.

Na pierw­szy rzut oka nie ma w tym niczego cie­ka­we­go, ani kon­tro­wer­syj­ne­go. Prze­cież równie dobrze mogli­by­śmy roz­dzie­lić parę ręka­wi­czek – i znów – kiedy w jednym pudle zna­leź­li­by­śmy prawą, to logicz­nie rzecz biorąc, w drugiej powinna znaj­do­wać się lewa. Problem w tym, że cząstki wcale nie zacho­wu­ją się jak ręka­wicz­ki i dotyczy ich pewna mocno nie­in­tu­icyj­na wła­sność świata kwantów, nazy­wa­na superpozycją.

Naj­pro­ściej mówiąc, obiekty sub­a­to­mo­we mogą znaj­do­wać się w wielu dostęp­nych stanach jed­no­cze­śnie. Cząstka pozo­sta­ją­ca w super­po­zy­cji może przy­kła­do­wo doko­ny­wać obrotu w dwóch prze­ciw­nych kie­run­kach, albo prze­by­wać w kilku miej­scach na raz (np. prze­miesz­czać się oby­dwo­ma ramio­na­mi inter­fe­ro­me­tru lub prze­cho­dzić przez dwie szcze­li­ny w prze­gro­dzie jed­no­cze­śnie). Brzmi to abs­trak­cyj­nie, bo prze­cież nikt nie widział samo­cho­du zmie­rza­ją­ce­go do celu wszyst­ki­mi ist­nie­ją­cy­mi drogami na raz – a w mikro­świe­cie mamy do czy­nie­nia właśnie z takimi sytu­acja­mi. Jednak co istotne: super­po­zy­cja nie jest wieczna i łatwo znika, kiedy tylko cząstka zosta­nie poddana pomia­ro­wi. Fizycy mówią w takiej sytu­acji o reduk­cji lub kolap­sie kwan­to­wej fali praw­do­po­do­bień­stwa, ozna­cza­ją­cej tyle, że badana cząstka skon­kre­ty­zo­wa­ła swój stan.

To zmienia bardzo wiele w kon­tek­ście naszego eks­pe­ry­men­tu myślo­we­go z pudeł­ka­mi. Ręka­wicz­ki byłyby twardo zde­fi­nio­wa­ne (lewa, prawa) już w momen­cie cho­wa­nia ich do pojem­ni­ków. Fotony nato­miast są w super­po­zy­cji; ich pola­ry­za­cja pozo­sta­je realnie nie­okre­ślo­na aż do momentu naszej inge­ren­cji. Zatem dopiero, kiedy otwie­ra­my jedno z pudeł, docho­dzi do meta­fo­rycz­ne­go rzutu monetą, a cząstka wybiera swój stan. A ponie­waż jest splą­ta­na z drugą cząstką, tamta również zostaje zmu­szo­na do auto­ma­tycz­ne­go skon­kre­ty­zo­wa­nia swojej pola­ry­za­cji. Jeżeli jedna cząstka okaże się spo­la­ry­zo­wa­na poziomo, to druga, nawet bez otwie­ra­nia pudła musi być spo­la­ry­zo­wa­na pionowo.

ZMIENNE UKRYTE? Porów­na­nie splą­ta­nych cząstek do pary ręka­wi­czek lub skar­pe­tek suge­ro­wa­ło­by, że cząstki mają swoje cechy (pola­ry­za­cje, spin itd.) jasno usta­lo­ne już w chwili wyemi­to­wa­nia ze źródła. W prze­szło­ści rze­czy­wi­ście zakła­da­no taką moż­li­wość, co dopro­wa­dzi­ło do naro­dzin teorii zmien­nych ukry­tych. Jednak póź­niej­sze eks­pe­ry­men­ty, zwłasz­cza doświad­cze­nia Alaina Aspecta (nagro­dzo­ne­go Noblem w 2022 roku) wyklu­czy­ły taką możliwość.

Kolaps szybszy od światła

Pewnie wiecie o tym, że for­mu­łu­jąc szcze­gól­ną teorię względ­no­ści, Albert Ein­ste­in posta­wił pewien warunek. Żeby jego wizja rela­tyw­ne­go czasu i prze­strze­ni dzia­ła­ła popraw­nie, założył, że pręd­kość światła w próżni powinna być nie­prze­kra­czal­ną stałą fizycz­ną. Żaden obiekt posia­da­ją­cy masę nie ma prawa dogonić pro­mie­nia światła, zaś samo światło porusza się dokład­nie w tempie 300 000 km/s.

Ogra­ni­cze­nie to dotyczy wszyst­kie­go, każdego oddzia­ły­wa­nia, nawet gra­wi­ta­cji. Gdyby nagle, z nie­zna­nych przy­czyn wypa­ro­wa­ło nasze Słońce, z uwagi na dzie­lą­cą nas odle­głość (150 mln kilo­me­trów), dowie­dzie­li­by­śmy się o tym nie szyb­ciej, niż po 8 minu­tach. Dopiero wtedy prze­sta­ły­by do nas docie­rać pro­mie­nie sło­necz­ne, a gra­wi­ta­cja gwiazdy prze­sta­ła­by utrzy­my­wać Ziemię na jej obecnej orbicie. Krótko mówiąc, we wszech­świe­cie wszyst­ko działa z pewnym opóźnieniem.

Wszyst­ko, poza splą­ta­niem kwantowym.

Właśnie z tego powodu Ein­ste­in, Podol­sky i Rosen byli mocno zanie­po­ko­je­ni. Wszyst­ko wska­zy­wa­ło na to, że splą­ta­ne cząstki są układem nie­lo­kal­nym. Pudła z foto­na­mi o splą­ta­nej pola­ry­za­cji możemy wysłać choćby na prze­ciw­ne krańce galak­ty­ki, albo nawet obser­wo­wal­ne­go wszech­świa­ta, a ich stany i tak pozo­sta­ną ściśle zwią­za­ne. Doko­nu­jąc pomiaru i usta­la­jąc pola­ry­za­cję jednego fotonu, stan dru­gie­go również zostaje zre­du­ko­wa­ny. Nie po upływie milio­nów lat czy paru godzin, ale w tej samej chwili. Więzi łączące ten układ są tak głę­bo­kie, że zdają się igno­ro­wać samą przestrzeń.

Tylko, czy aby na pewno jest to wyłom od postu­la­tów szcze­gól­nej teorii względ­no­ści? A jeśli tak, to czy splą­ta­nie kwan­to­we może nam posłu­żyć do natych­mia­sto­wej, nad­świetl­nej komunikacji?

Kwantowe wiadomości

Wbrew temu, o czym przed chwilą się dowie­dzie­li­śmy, ein­ste­inow­ska wizja cza­so­prze­strze­ni jest bez­piecz­na. Autor teorii względ­no­ści obawiał się głównie róż­no­ra­kich para­dok­sów i zabu­rzeń przy­czy­no­wo-skut­ko­wych, wyni­ka­ją­cych z szansy pro­pa­go­wa­nia wia­do­mo­ści i oddzia­ły­wań z nie­ogra­ni­czo­ną pręd­ko­ścią. Jednak wszyst­ko wska­zu­je na to, że układ splą­ta­ny nie prze­sy­ła żadnej infor­ma­cji. W każdym razie, nie prak­tycz­nym zna­cze­niu tego słowa.

Ktoś mógłby wpaść na projekt kwan­to­we­go komu­ni­ka­to­ra, gdzie cząstka spo­la­ry­zo­wa­na pod danym kątem to umownie jakaś litera. Wtedy, obie strony posia­da­ją­ce po jednym zesta­wie splą­ta­nych fotonów, mogłyby bły­ska­wicz­nie wymie­niać wia­do­mo­ści. Wszyst­ko odby­wa­ło­by się bły­ska­wicz­nie i bez względu na dzie­lą­cy użyt­kow­ni­ków dystans.

Brzmi nieźle, ale pomysł zadzia­ła tylko na papie­rze i tylko wtedy, kiedy pomi­nie­my abso­lut­ny fizycz­ny fun­da­ment. Zja­wi­sko super­po­zy­cji. Pod­kreśl­my to raz jeszcze: cząstki są mie­sza­ni­ną stanów (np. różnych pola­ry­za­cji), a my nie mamy żadnego wpływu na to, jaki stan wybie­rze cząstka w chwili pomiaru. Nie ist­nie­je metoda, która pozwo­li­ła­by nam zmusić foton do wyboru pola­ry­za­cji pio­no­wej i jed­no­cze­sne­go prze­sta­wie­nia fotonu part­ne­ra do pozycji prze­ciw­nej. Nie mani­pu­lu­je­my stanami cząstki, jedynie spraw­dza­my jej stan i mamy 50% szans na jedną opcję i 50% na drugą. To kom­plet­nie niweczy nasz sprytny plan. Bez kon­tro­li nad kwan­to­wą super­po­zy­cją, z natury losową, możemy prze­słać co naj­wy­żej przy­pad­ko­wy ciąg znaków. W tej sytu­acji, nawet napi­sa­nie zwy­kłe­go “cześć”, nie wchodzi w grę.

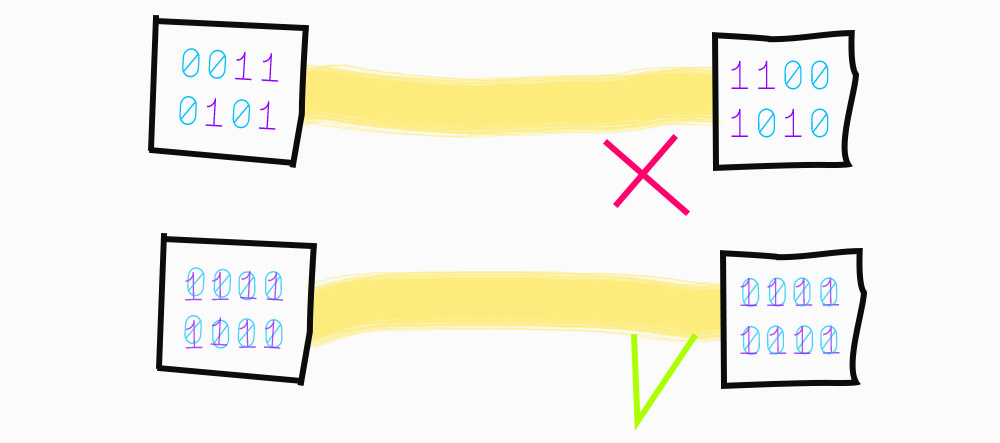
Nie oznacza to nato­miast, że sam efekt splą­ta­nia pozo­sta­je dla nas zupeł­nie bez­u­ży­tecz­ny. Te same pra­wi­dła mecha­ni­ki kwan­to­wej, które nie pozwa­la­ją na nad­świetl­ną komu­ni­ka­cję, dają nam obiet­ni­cę opra­co­wa­nia kom­pu­te­rów kwan­to­wych oraz nowych metod szy­fro­wa­nia. To właśnie deli­kat­ny stan super­po­zy­cji jest kluczem do jed­no­cze­sne­go, super­szyb­kie­go wyko­ny­wa­nia wielu ope­ra­cji mate­ma­tycz­nych na raz, jak również pod­sta­wą dla zabez­pie­czeń nie­moż­li­wych do zła­ma­nia, bez znisz­cze­nia samej wiadomości.

W ten czy inny sposób, stoimy u progu rewo­lu­cji kwan­to­wej i wszyst­ko wska­zu­je na to, że zja­wi­sko splą­ta­nia będzie jej głównym motorem napędowym.