6 odkryć naukowych inspirowanych jedzeniem

Każda kuchnia to w pewnym sensie małe, domowe labo­ra­to­rium. Z kolei sam proces goto­wa­nia to nic innego, aniżeli ciąg pro­stych fizycz­no-che­micz­nych eks­pe­ry­men­tów. Nie dziwi więc, że obser­wa­cje zwy­kłych potraw oraz pospo­li­tych kuli­nar­nych czyn­no­ści, tak często napro­wa­dza­ły (i nadal napro­wa­dza­ją) uczo­nych na trop zupeł­nie poważ­nych zjawisk, pro­ce­sów i hipotez. 

Łamanie makaronu

Zacznij­my z przy­tu­pem, od nobli­sty i kone­se­ra bon­go­sów, Richar­da Feyn­ma­na. Z bio­gra­fią sław­ne­go fizyka wiąże się wiele cie­ka­wych anegdot, a jedna z bar­dziej poucza­ją­cych dotyczy… spa­ghet­ti. Rzecz miała miejsce podczas kolacji, na którą nauko­wiec spędził ze swoim kumplem – infor­ma­ty­kiem z MIT – Danie­lem Hillisem.

Podobno panowie nie mogli znaleźć w kuchni dosyć dużego gara, żeby zmie­ścić w nim długi makaron, więc podjęli męską decyzję o jego poła­ma­niu (łamiąc przy okazji serca milio­nom Włochów). Przy tej pro­za­icz­nej czyn­no­ści Feynman spo­strzegł, że spa­ghet­ti pęka w bardzo spe­cy­ficz­ny sposób. Gdy­by­śmy zostali zapy­ta­ni, jak powinno wyglą­dać pęk­nię­cie długiej, sztyw­nej tyczki, zapewne odpo­wie­dzie­li­by­śmy, że mniej więcej w połowie złamie się na dwie części. Tym­cza­sem przy­pad­ko­wa obser­wa­cja wyka­za­ła, że sucha nić maka­ro­nu z jakie­goś powodu, naj­czę­ściej rozpada się na trzy kawałki. Hillis wspo­mi­na, że tamtego wie­czo­ru poła­ma­li jeszcze wiele paczek spa­ghet­ti, ale ani nie wyja­śni­li dziw­ne­go zja­wi­ska, ani nie zaspo­ko­ili apetytu.

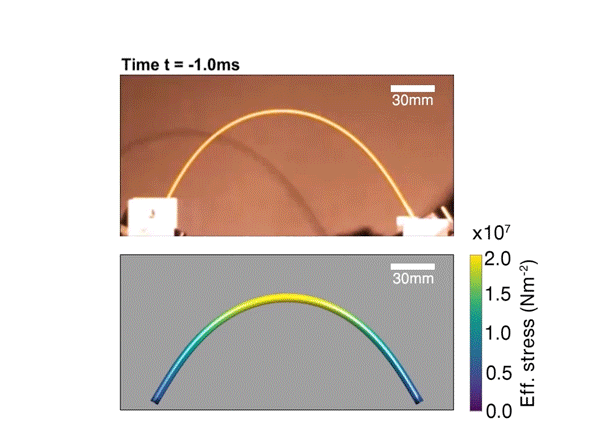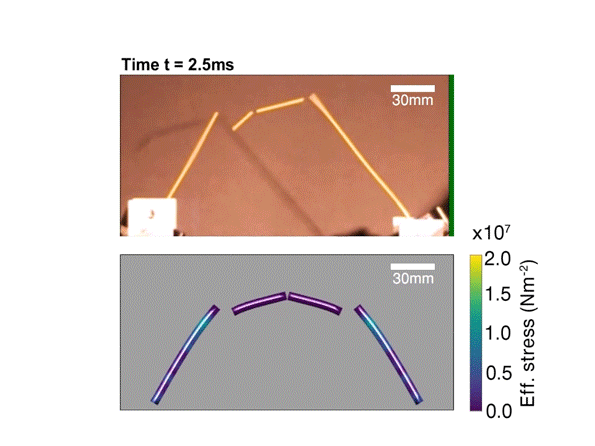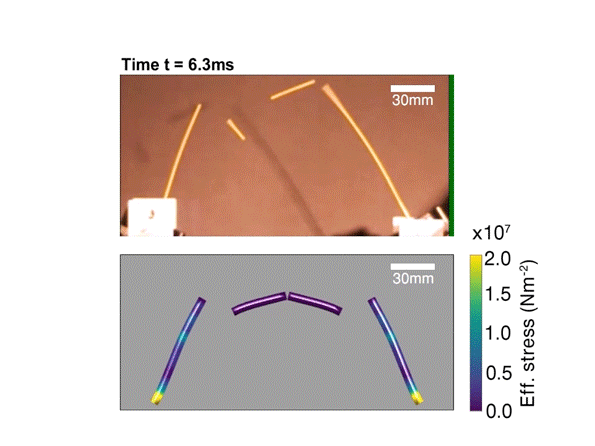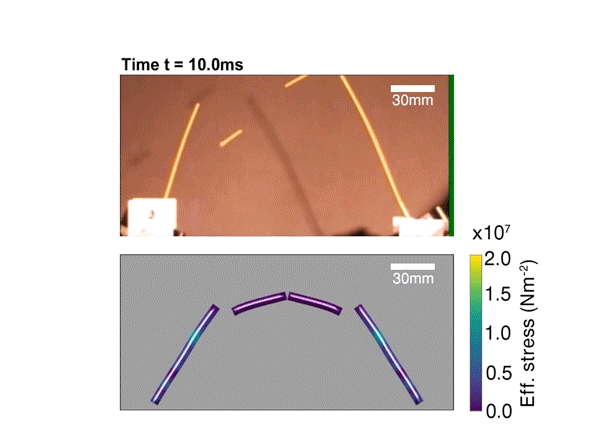
Maka­ro­no­wa zagadka stała się realnym przed­mio­tem badań fizycz­nych, ale prze­ko­nu­ją­ca odpo­wiedź poja­wi­ła się dopiero w 2005 roku, sie­dem­na­ście lat po śmierci Feyn­ma­na. Fran­cu­zi Basile Audoly oraz Séba­stien Neu­kirch stwier­dzi­li, że roz­wią­za­nie kryje się na etapie pro­sto­wa­nia, tuż po wystą­pie­niu pierw­sze­go pęk­nię­cia. W pobliżu przy­trzy­my­wa­nej koń­ców­ki, nitka pro­sto­wa­ła się szyb­ciej niż na innych odcin­kach, co tworzy dość silną falę pro­wa­dzą­cą – zależ­nie od dłu­go­ści i gru­bo­ści obiektu – do kolej­nych złamań.

Paradoks liści herbaty

Był Feynman, to teraz dajmy szansę Alber­to­wi Ein­ste­ino­wi. Nazwi­sko tego legen­dar­ne­go uczo­ne­go koja­rzy­my głównie z wiel­ki­mi roz­wa­ża­nia­mi nad naturą cza­so­prze­strze­ni, jednak i jemu zda­rza­ło się pochy­lać nad całkiem przy­ziem­ny­mi pro­ble­ma­mi. Tak było w 1926 roku, kiedy opu­bli­ko­wał artykuł opi­su­ją­cy zacho­wa­nie liści w fili­żan­ce herbaty (zawsty­dza­jąc tym samym herbaciarzy-Brytyjczyków).

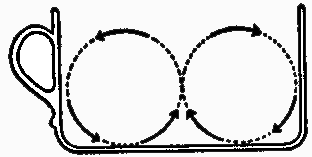
Ein­ste­ina zasta­na­wia­ła skłon­ność listków do zbie­ra­nia się pośrod­ku wiru­ją­cej wody. Prze­cież siła odśrod­ko­wa powinna raczej wypy­chać je ku brzegom naczy­nia. Fizyk doszedł do wniosku, że roz­wią­za­nia należy szukać nie na powierzch­ni płynu, lecz w głębi. Tarcie herbaty o dno fili­żan­ki wywo­łu­je zmiany w ciśnie­niu, które tłumi siłę wiru i ściąga listki do środka. 

Niby nic wiel­kie­go, ale ta skromna obser­wa­cja prze­ło­ży­ła się na dzie­siąt­ki prac z zakresu fizyki atmos­fe­ry, hydro­lo­gii, a nawet medy­cy­ny. Przy­kła­do­wo, w 2007 roku her­ba­cia­na fizyka zain­spi­ro­wał Austra­lij­czy­ków do opra­co­wa­nia nowa­tor­skiej metody szyb­kiej i wydaj­nej sepa­ra­cji osocza krwi na pozio­mie mikroskopowym.

Jak szybko rozchodzi się dźwięk w serze?

W 1999 roku grupa hisz­pań­skich naukow­ców – Antonio Mulet, Jose Bene­di­to, José Bon oraz Carmen Ros­sel­lo – posta­wi­ła spraw­dzić, czy da się okre­ślić zmiany tem­pe­ra­tu­ry wnętrza sera, poprzez prze­pusz­cze­nie przez nią fal dźwię­ko­wych o niskiej czę­sto­tli­wo­ści. Eks­pe­ry­men­ty prze­pro­wa­dzo­ne na bryle angiel­skie­go czedaru wyka­za­ły, że jak naj­bar­dziej. Z publi­ka­cji zamiesz­czo­nej na łamach Journal of Food Science możemy się dowie­dzieć, że w tem­pe­ra­tu­rach od 0°C do 35°C pręd­kość ultra­dź­wię­ków wahała się od 1590 do 1696 m/s. Autorzy usta­li­li również, że głównym czyn­ni­kiem jest topie­nie tłuszczu.

Wbrew pozorom nie była to zabawa, lecz pokaz moż­li­wo­ści bardzo prak­tycz­nej metody bez­in­wa­zyj­nej kon­tro­li struk­tu­ry sera, która rze­czy­wi­ście zna­la­zła zasto­so­wa­nie u nie­któ­rych pro­du­cen­tów wyso­ko­ja­ko­ścio­wej żyw­no­ści. Hisz­pa­nie zostali także doce­nie­ni przez komisję Ig Nobli (czyli tych śmiesz­niej­szych Nobli), otrzy­mu­jąc wyróż­nie­nie w dzie­dzi­nie chemii za rok 2006.

Spadające tosty z masłem

O ile nie każdy zdaje sobie sprawę ze spe­cy­ficz­ne­go pękania nitek spa­ghet­ti, o tyle nie ma chyba osoby, która na pewnym etapie życia nie zadała sobie pytania: dla­cze­go ta cho­ler­na kanapka musiała spaść ze stołu akurat posma­ro­wa­ną stroną ku pod­ło­dze? Kwestię tę ze śmier­tel­ną powagą potrak­to­wa­li uczeni z Man­che­ste­ru, oglą­da­jąc dla dobra nauki aż sto upadków tostów z masłem.

Bry­tyj­czy­cy potwier­dzi­li, że chleb rze­czy­wi­ście znacz­nie chęt­niej ląduje górą do dołu, ale jed­no­cze­śnie obalili naj­prost­sze wytłu­ma­cze­nie tego zja­wi­ska, zgodnie z którym zna­cze­nie miałby większy ciężar posma­ro­wa­nej powierzch­ni. Stan­dar­do­wa warstwa masła (czy cze­go­kol­wiek czym uroz­ma­ica­cie sobie śnia­da­nie) nie ma prak­tycz­ne­go wpływu na prze­bieg lotu tostu. Zdaniem autorów badania, głównym wino­waj­cą jest stół – a dokład­niej jego wyso­kość. Strą­co­na z blatu kromka obraca się w powie­trzu, a dystans około 1 metra to akurat tyle, żeby zdążyła zmienić swoją pozycję o 180 stopni i plasnąć swoją górą (zwykle posma­ro­wa­ną) w parkiet. Gdy­by­śmy mocno zwięk­szy­li wyso­kość stołu, powiedz­my do trzech metrów, tost zdo­łał­by wykonać pełny obrót i sta­ty­stycz­nie czę­ściej lądo­wał­by masłem do góry. Nie­ste­ty wygoda korzy­sta­nia z takiego stołu stoi pod dużym znakiem zapytania.

Twierdzenie o pizzy

Przejdź­my teraz do spraw napraw­dę poważ­nych. Jak dokonać spra­wie­dli­we­go podzia­łu pizzy? Nie jest to problem, jeśli uda nam się zlo­ka­li­zo­wać sam środek koli­ste­go ciasta i wszyst­kie linie prze­pro­wa­dzi­my przez ten punkt. Ale co w momen­cie, kiedy się pomy­li­my, doko­nu­jąc kiep­skie­go pierw­sze­go cięcia? 

O mniej­sze rzeczy wybu­cha­ły bójki, na szczę­ście tu z pomocą przy­cho­dzi mate­ma­tycz­ne twier­dze­nie o pizzy. Zgodnie z nim, żeby ura­to­wać sytu­ację wystar­czy podzie­lić koło na osiem lub większą (ale koniecz­nie podziel­ną przez cztery) liczbę frag­men­tów, tak żeby wszyst­kie linie prze­ci­na­ły się w jednym punkcie w obrębie koła. I voilà! Powierzch­nia kawał­ków 1, 3, 5 i 7 równa się powierzch­ni frag­men­tów ozna­czo­nych 2, 4, 6 i 8. For­mal­ne­go potwier­dze­nia powyż­sze­go twier­dze­nia dostar­czy­li Rick Mabry i Paul Deier­mann w arty­ku­le z 2009 roku pt. O serze i cieście: dowód na teorię pizzy i inne smaczne rezul­ta­ty.

Podobno metoda spraw­dza się równie sku­tecz­nie w przy­pad­ku każdego gatunki pizzy, a nawet okrą­głe­go ciasta z nało­żo­nym ananasem.

Lody Mpemby

Erasto Mpemba był tan­zań­skim nasto­lat­kiem, który dora­biał sprze­da­jąc lody i prze­szedł do histo­rii zabi­ja­jąc ćwieka fizykom. Afry­kań­czyk zauwa­żył, że kiedy dla zaosz­czę­dze­nia czasu wsadzał do zamra­żar­ki mleczną mie­sza­ni­nę jeszcze ciepłą, bez cze­ka­nia na jej osty­gnię­cie, zama­rza­ła ona ona szyb­ciej niż zwykle. Tak napraw­dę ową nie­lo­gicz­ność opi­sy­wa­li już wcze­śniej Ary­sto­te­les i Kar­te­zjusz, ale dopiero Mpemba zwrócił na nią uwagę współ­cze­snej nauki. W prze­ku­ciu prostej obser­wa­cji w poważną publi­ka­cję pomógł mło­dzień­co­wi, prze­by­wa­ją­cy w okolicy bry­tyj­ski nauczy­ciel i dyplo­ma­ta, Denis Osborne. “Nazywam się Erasto B. Mpemba i mam zamiar opo­wie­dzieć o moim odkry­ciu, które było spo­wo­do­wa­ne nie­wła­ści­wym użyt­ko­wa­niem lodówki…” – głosiło pierw­sze zdanie arty­ku­łu z 1969 roku.

Mpemba i Osborne raczej nie sądzili, że sfor­mu­ło­wa­ny przez nich problem, będzie roz­wa­ża­ny jeszcze długo po ich śmierci. Tym­cza­sem efekt Mpemby wraca jak bume­rang, towa­rzy­sząc kolej­nym hipo­te­zom z zakresu ter­mo­dy­na­mi­ki i prze­mian fazo­wych, publi­ko­wa­nym m.in. na łamach Nature, Phy­si­cal Review, czy PNAS – ogra­ni­cza­jąc się jedynie do nie­daw­nych numerów naj­bar­dziej reno­mo­wa­nych bran­żo­wych perio­dy­ków. Kto by pomy­ślał, że zwykłe lody i na pozór pospo­li­te zja­wi­sko zama­rza­nia, okażą się taką zmorą dla teo­re­ty­ków, nawet w XXI wieku?